11.0 第11章 堆与优先级队列 11.1 堆的概念与算法

第11章 堆与优先级队列

前面两章介绍了Java中的基本容器类，每个容器类背后都有一种数据结构，ArrayList是动态数组，LinkedList是链表，HashMap/HashSet是哈希表，TreeMap/TreeSet是红黑树，本章介绍另一种数据结构：堆。之前我们提到过堆，那里，堆指的是内存中的区域，保存动态分配的对象，与栈相对应。这里的堆是一种数据结构，与内存区域和分配无关。

堆到底是什么结构呢？这个待会再细看。我们先来说明，堆有什么用？为什么要介绍它？堆可以非常高效方便地解决很多问题，比如：
1）优先级队列，我们之前介绍的队列实现类LinkedList是按添加顺序排列的，但现实中，经常需要按优先级来，每次都应该处理当前队列中优先级最高的，高优先级的即使来得晚，也应该被优先处理。
2）求前K个最大的元素，元素个数不确定，数据量可能很大，甚至源源不断到来，但需要知道到目前为止的最大的前K个元素。这个问题的变体有：求前K个最小的元素，求第K个最大的元素，求第K个最小的元素。
3）求中值元素，中值不是平均值，而是排序后中间那个元素的值，同样，数据量可能很大，甚至源源不断到来。

堆还可以实现排序，称之为堆排序，不过有比它更好的排序算法，所以，我们就不介绍其在排序中的应用了。

Java容器中有一个类PriorityQueue，表示优先级队列，它实现了堆，本章我们会详细介绍。关于如何使用堆高效解决求前K个最大的元素和求中值元素，我们也会在本章中用代码实现并详细解释。

说了这么多好处，堆到底是什么呢？我们先来看堆的基本概念与算法。

11.1 堆的概念与算法

我们先来了解堆的概念，然后介绍堆的一些主要算法。

堆首先是一棵二叉树，但它是完全二叉树。什么是完全二叉树呢？我们先来看另一个相似的概念：满二叉树。满二叉树是指除了最后一层外，每个节点都有两个孩子，而最后一层都是叶子节点，都没有孩子。比如，图11-1所示两棵二叉树都是满二叉树。

图11-1 满二叉树示例

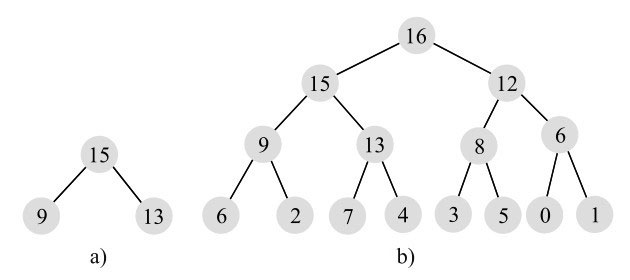
满二叉树一定是完全二叉树，但完全二叉树不要求最后一层是满的，但如果不满，则要求所有节点必须集中在最左边，从左到右是连续的，中间不能有空的。比如，图11-2所示几棵二叉树都是完全二叉树。

图11-2 完全二叉树示例

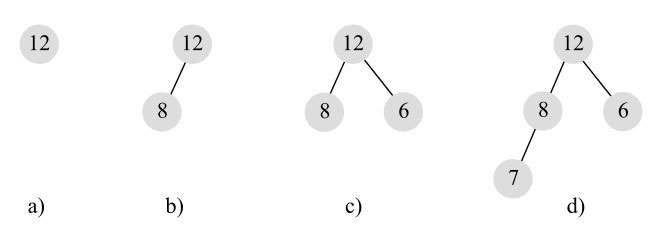
而图11-3所示的几棵二叉树则都不是完全二叉树。

图11-3 非完全二叉树示例

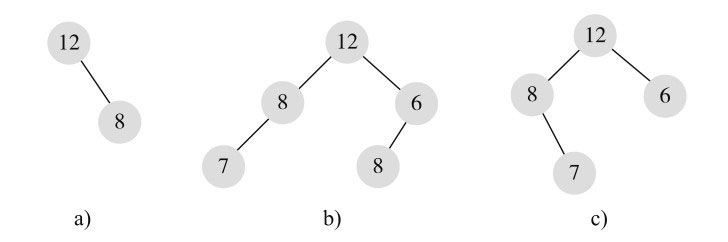
在完全二叉树中，可以给每个节点一个编号，编号从1开始连续递增，从上到下，从左到右，如图11-4所示。

完全二叉树有一个重要的特点：给定任意一个节点，可以根据其编号直接快速计算出其父节点和孩子节点编号。如果编号为i，则父节点编号即为i/2，左孩子编号即为2× i，右孩子编号即为2× i+1。比如，对于5号节点，父节点为5/2即2，左孩子为2× 5即10，右孩子为2× 5+1即11。

图11-4 完全二叉树编号

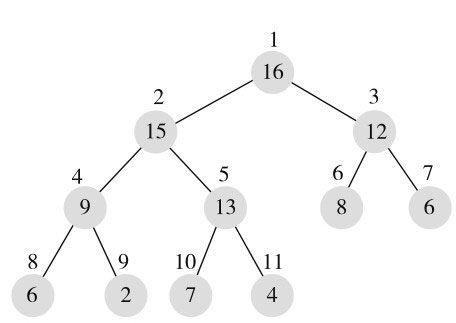
这个特点为什么重要呢？它使得逻辑概念上的二叉树可以方便地存储到数组中，数组中的元素索引就对应节点的编号，树中的父子关系通过其索引关系隐含维持，不需要单独保持。比如，图11-4所示的逻辑二叉树，保存到数组中，其结构如图11-5所示。

图11-5 用数组表示完全二叉树

父子关系是隐含的，比如对于第5个元素13，其父节点就是第2个元素15，左孩子就是第10个元素7，右孩子就是第11个元素4。

这种存储二叉树的方法与之前介绍的TreeMap是不一样的。在TreeMap中，有一个单独的内部类Entry, Entry有三个引用，分别指向父节点、左孩子、右孩子。使用数组存储的优点是节省空间，而且访问效率高。堆逻辑概念上是一棵完全二叉树，而物理存储上使用数组，还有一定的顺序要求。

之前介绍过排序二叉树。排序二叉树是完全有序的，每个节点都有确定的前驱和后继，而且不能有重复元素。与排序二叉树不同，在堆中，可以有重复元素，元素间不是完全有序的，但对于父子节点之间，有一定的顺序要求。根据顺序分为两种堆：一种是最大堆，另一种是最小堆。

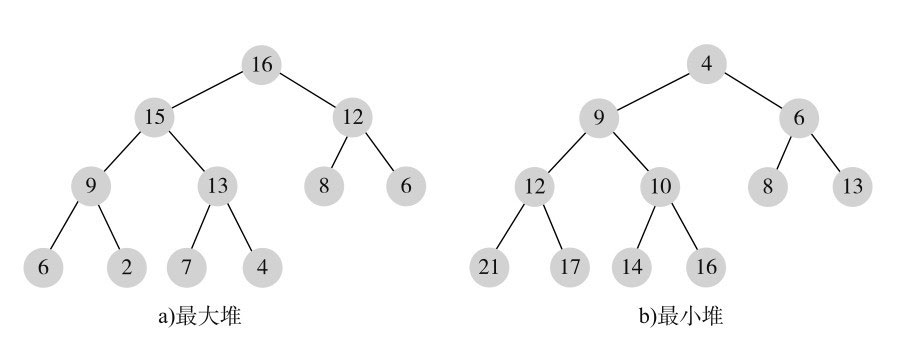
最大堆是指每个节点都不大于其父节点。这样，对每个父节点，一定不小于其所有孩子节点，而根节点就是所有节点中最大的，对每个子树，子树的根也是子树所有节点中最大的。最小堆与最大堆正好相反，每个节点都不小于其父节点。这样，对每个父节点，一定不大于其所有孩子节点，而根节点就是所有节点中最小的，对每个子树，子树的根也是子树所有节点中最小的。我们看个例子，如图11-6所示。

总结来说，逻辑概念上，堆是完全二叉树，父子节点间有特定顺序，分为最大堆和最小堆，最大堆根是最大的，最小堆根是最小的，堆使用数组进行物理存储。

为什么堆可以高效地解决之前我们说的问题呢？在回答之前，我们需要先看下，如何在堆上进行数据的基本操作，在操作过程中如何保持堆的属性不变。

图11-6 最大堆与最小堆示例

11.1.2 堆的算法

下面，我们介绍如何在堆上进行数据的基本操作。最大堆和最小堆的算法是类似的，我们以最小堆来说明。先来看如何添加元素。

1．添加元素

如果堆为空，则直接添加一个根就行了。我们假定已经有一个堆，要在其中添加元素，基本步骤为：

1）添加元素到最后位置。
2）与父节点比较，如果大于等于父节点则满足堆的性质，结束，否则与父节点进行交换，然后再与父节点比较和交换，直到父节点为空或者大于等于父节点。

图11-7 堆的算法示例：添加元素前的初始结构

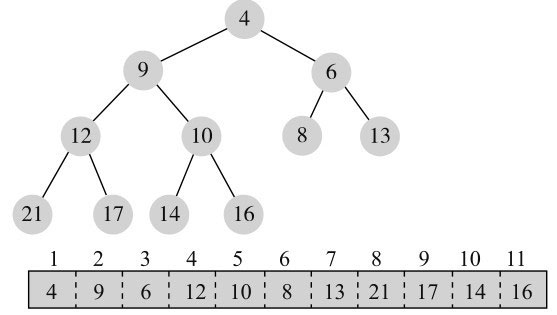
我们来看个例子。图11-7是添加元素前的初始结构。

添加元素3，第一步后，结构如图11-8所示。

图11-8 堆的算法示例：添加元素3第一步后的结构

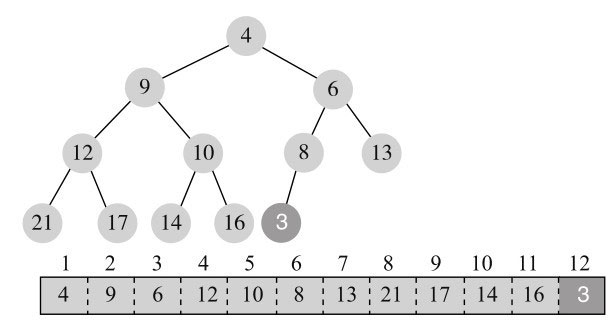
3小于父节点8，不满足最小堆的性质，所以与父节点交换，变为图11-9所示。

图11-9 堆的算法示例：添加元素3第一次交换后的结构

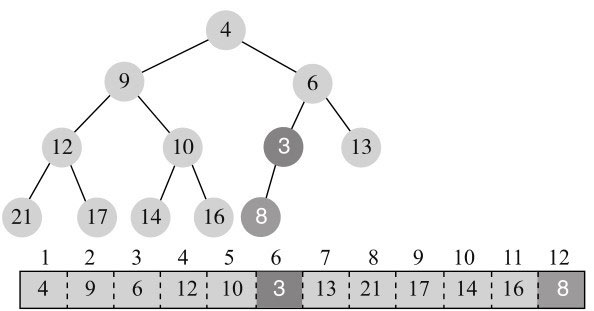
交换后，3还是小于父节点6，所以继续交换，变为图11-10所示。

图11-10 堆的算法示例：添加元素3第二次交换后的结构

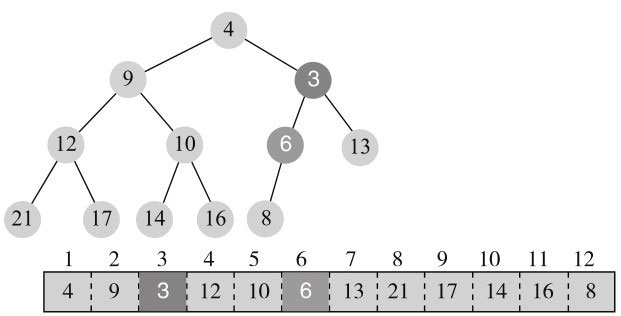
交换后，3还是小于父节点，也是根节点4，继续交换，变为图11-11所示。

图11-11 堆的算法示例：添加元素3第三次交换后的结构

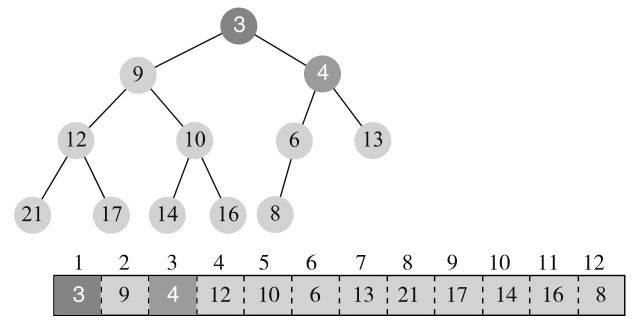
至此，调整结束，树保持了堆的性质。

从以上过程可以看出，添加一个元素，需要比较和交换的次数最多为树的高度，即log2(N), N为节点数。这种自底向上比较、交换，使得树重新满足堆的性质的过程，我们称为向上调整（siftup）。

2．从头部删除元素

在队列中，一般是从头部删除元素，Java中用堆实现优先级队列。下面介绍如何在堆中删除头部，其基本步骤为：
1）用最后一个元素替换头部元素，并删掉最后一个元素；
2）将新的头部与两个孩子节点中较小的比较，如果不大于该孩子节点，则满足堆的性质，结束，否则与较小的孩子节点进行交换，交换后，再与较小的孩子节点比较和交换，一直到没有孩子节点，或者不大于两个孩子节点。这个过程称为向下调整（siftdown）。

我们来看个例子。图11-12是删除元素前的初始结构。

图11-12 堆的算法示例：删除元素前的初始结构

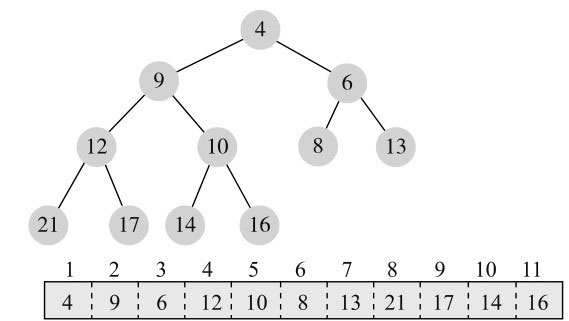
执行第一步，用最后元素替换头部，如图11-13所示。

图11-13 堆的算法示例：删除头部元素第一步后的结构

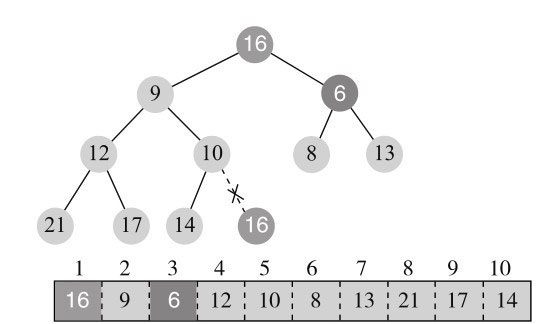
现在根节点16大于孩子节点，与更小的孩子节点6进行替换，结构变为图11-14所示。

图11-14 堆的算法示例：删除头部元素第一次交换后的结构

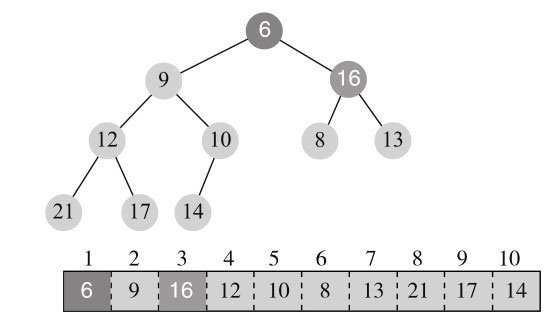
16还是大于孩子节点，与更小的孩子8进行交换，结构如图11-15所示。

图11-15 堆的算法示例：删除头部元素第二次交换后的结构

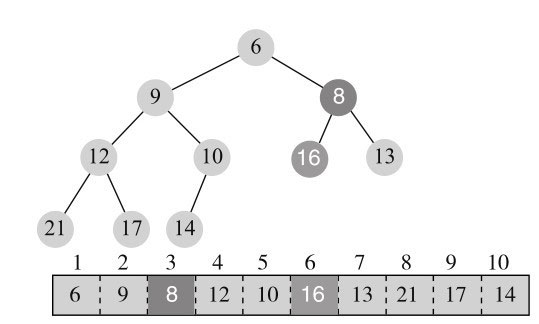
至此，就满足堆的性质了。

3．从中间删除元素

那如果需要从中间删除某个节点呢？与从头部删除一样，都是先用最后一个元素替换待删元素。不过替换后，有两种情况：如果该元素大于某孩子节点，则需向下调整（sift-down）；如果小于父节点，则需向上调整（siftup）。

我们来看个例子，删除值为21的节点，第一步如图11-16所示。

图11-16 堆的算法示例：从中间删除元素21第一步后的结构

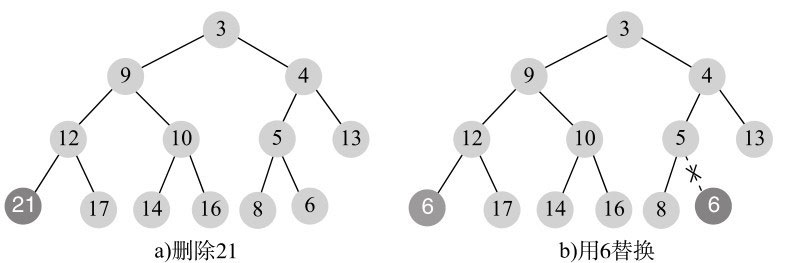
替换后，6没有子节点，小于父节点12，执行向上调整（siftup）过程，最后结果如图11-17所示。

图11-17 堆的算法示例：从中间删除元素21调整后的结构

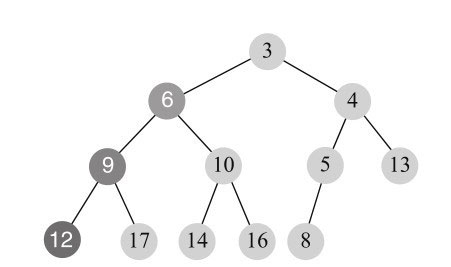
我们再来看个例子，删除值为9的节点，第一步如图11-18所示。

图11-18 堆的算法示例：从中间删除元素9第一步后的结构

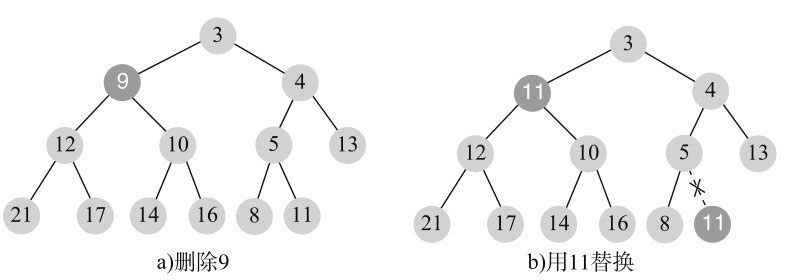
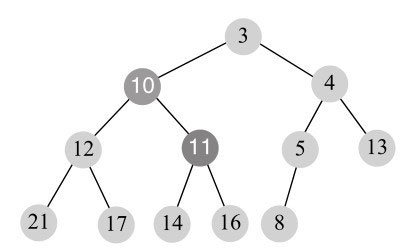
交换后，11大于右孩子10，所以执行向下调整（siftdown）过程，执行结束后如图11-19所示。

图11-19 堆的算法示例：从中间删除元素9调整后的结构

4．构建初始堆

给定一个无序数组，如何使之成为一个最小堆呢？将普通无序数组变为堆的过程称为heapify。基本思路是：从最后一个非叶子节点开始，一直往前直到根，对每个节点，执行向下调整（siftdown）。换句话说，是自底向上，先使每个最小子树为堆，然后每对左右子树和其父节点合并，调整为更大的堆，因为每个子树已经为堆，所以调整就是对父节点执行向下调整（siftdown），这样一直合并调整直到根。这个算法的伪代码是：

void heapify() {
    for(int i=size/2; i >= 1; i--)
        siftdown(i);
}

size表示节点个数，节点编号从1开始，size/2表示第一个非叶子节点的编号。

这个构建的时间效率为O(N), N为节点个数，具体就不证明了。

5．查找和遍历

在堆中进行查找没有特殊的算法，就是从数组的头找到尾，效率为O(N)。

在堆中进行遍历也是类似的，堆就是数组，堆的遍历就是数组的遍历，第一个元素是最大值或最小值，但后面的元素没有特定的顺序。

需要说明的是，如果是逐个从头部删除元素，那么堆可以确保输出是有序的。

6．算法小结

以上就是堆操作的主要算法，小结如下。
1）在添加和删除元素时，有两个关键的过程以保持堆的性质，一个是向上调整（siftup），另一个是向下调整（siftdown），它们的效率都为O(log2(N))。由无序数组构建堆的过程heapify是一个自底向上循环的过程，效率为O(N)。
2）查找和遍历就是对数组的查找和遍历，效率为O(N)。

11.1.3 小结

本节介绍了堆这一数据结构的基本概念和算法。堆是一种比较神奇的数据结构，概念上是树，存储为数组，父子有特殊顺序，根是最大值/最小值，构建/添加/删除效率都很高，可以高效解决很多问题。但在Java中，堆到底是如何实现的呢？本章开头提到的那些问题，用堆到底如何解决呢？让我们在接下来的小节中继续探讨。