LaTex 常用语法
公式显示位置
行内公式
在公式两边各自加上一个美元符号即使行内公式
1 | 这是文本$a^2+b^2=c^2$这是文本 |
显示效果:
这是文本$a^2+b^2=c^2$这是文本
行间公式
在公式两边各自加上两个美元符号即使行将公式:
1 | 这是文本$$a^2+b^2=c^2$$这是文本 |
显示效果:
这是文本$$a^2+b^2=c^2$$这是文本
数学符号
上下标
在LaTex中用^和_表明上下标。注意如果上下标只对其后面的一个字符起作用,如果上下标的内容超过一个字符,则需要用花括号{}包裹,否则上下标只对后面的一个符号起作用
1 | $$p^3_{ij}\qquad\sum_{K=1}^3ka^x+y\qquad\neq a^{x+y}$$ |
显示效果:
$$p^3_{ij}\qquad\sum_{K=1}^3ka^x+y\qquad\neq a^{x+y}$$
导数符号
导数符号'是一个特殊的上标,可以适当连用表示多阶导数,也可以在其后连用上标:
1 | $f(x)=x^2 \quad f'(x)=2x \quad f''^{2}=4$ |
显示效果:
$f(x)=x^2 \quad f’(x)=2x \quad f’’^{2}=4$
偏导 条件偏导
偏导符号$\partial$
1 | $\left.\frac{\partial f(x,y)}{\partial x}\right|_{x=0}$ |
$\left.\frac{\partial f(x,y)}{\partial x}\right|_{x=0}$
分式
如果是简单的根式,可以写成斜分式的形式,如3/8:,在latex中分式一般使用\frac{分子}{分母}来书写。不过这种分式的大小在行间公式是正常显示大小,而在行内被极度压缩了。amsmath提供了方便的命令\dfrac{分子}{分母}和\tfrac{分子}{分母},令用户能够在行内使用正常大小的行内公式。
显示效果:
1 | 斜分式: $3/8 \qquad $,压缩分式:$\frac{3}{8}\qquad$ ,显示正常大小:$\dfrac{3}{8}$ |
斜分式: $3/8 \qquad $,压缩分式:$\frac{3}{8}\qquad$ ,显示正常大小:$\dfrac{3}{8}$
根式
一般的根式使用\sqrt{…}表示,表示n此方根式写成\sqrt[n]{…}:
1 | $\sqrt{x} \Leftrightarrow x^{1/2} |
显示效果:
$\sqrt{x} \Leftrightarrow x^{1/2}
\quad \sqrt[3]{2}
\quad \sqrt{x^{2}+\sqrt{y}}
$
特殊的分式形式,如二项式结构,由amsmath宏包的\binom命令生成:
1 | Pascal's rule is |
Pascal’s rule is
$$
\binom{n}{k}=\binom{n-1}{k}+\binom{n-1}{k-1}
$$
无穷大符号
1 | $\infty$ |
$\infty$
这个是个缩写,原单词(infinity)读音:
省略号
| 名称 | 符号 | 效果 |
|---|---|---|
| 水平省略号 | \dots | $\dots$ |
| 水平省略号 | \cdots | $\cdots$ |
| 竖直省略号 | \vdots | $\vdots$ |
| 斜排省略号 | \ddots | $\ddots$ |
1 | $a_1,a_2,\dots,a_n$ |
显示效果如下:
$a_1,a_2,\dots,a_n$
$a_1,a_2,\cdots,a_n$
\cdots和\dots是完全等效的,它们既能用在公式中,也用在文本里作为省略号。
除此之外,在矩阵中可能会用到竖排的$\vdots$(\vdots)和斜排的$\ddots$(\ddots)
关系符
LaTex常见的关系符号除了可以直接输入的=,>,<,其他符号用命令输入,常用的有不等于: $\ne$ (\ne),大于等于号: $\ge$ (\ge)和小于等于号:$\le$ (\le),约等于号: $\approx$ (\approx),等价 $\equiv$ (\equiv),正比: $\propto$ (\propto),相似: $\sim$ (\sim)等等。
LaTex还提供了自定义二元关系符的命令\stackrel,用于将一个符号叠加在原有的二元关系符之上:
1 | $$ |
$$
f_n(x) \stackrel{*}{\approx} 1
$$
巨算子
积分号,求和号等符号称为**巨算子**。
| 名称 | 符号 | 效果 |
|---|---|---|
| 积分号 | \int | $\int$ |
| 求和号 | \sum | $\sum$ |
1 | $$ |
$$
\sum_{i=1}^n \quad
\int_0^{\frac{\pi}{2}} \quad
\oint_0^{\frac{\pi}{2}} \quad
\prod_\epsilon
$$
巨算符的上下标用作其上下限。行间公式中,积分号默认将上下限放在右上角和右下角,求和号默认在上下方;行内公式一律默认在右上角和右下角。可以在巨算符后使用\limits手动令上下限显示在上下方,\nolimits则相反,即不显示在上下方,也就是显示在右上角,右下角。
1 | $$ |
$$
\sum\nolimits_{i=1}^n \quad
\int\limits_0^{\frac{\pi}{2}} \quad
\prod\nolimits_\epsilon
$$
极限符号
行间公式极限
行间公式下标默认放在符号的下方,所以直接再极限符号\lim下方写上符号极限范围即可:
1 | $${\lim_{x \to +\infty}}$$ |
$${\lim_{x \to +\infty}}$$
1 | $${\lim_{x \to -\infty}}$$ |
$${\lim_{x \to -\infty}}$$
1 | $${\lim_{x \to 0}}$$ |
$${\lim_{x \to 0}}$$
1 | $${\lim_{x \to 0^+}}$$ |
$${\lim_{x \to 0^+}}$$
1 | $${ \lim_{x \to 0} \frac{3x^2 +7x^3}{x^2 +5x^4} = 3}$$ |
$${ \lim_{x \to 0} \frac{3x^2 +7x^3}{x^2 +5x^4} = 3}$$
行间极限
行间的下标默认放在右下角,可以使用\limits_{下标}把下标放到符号下方即可。实例如下所示:
1 | ${\lim \limits_{x \to -\infty}}$ |
行间极限符号:${\lim \limits_{x \to -\infty}}$
集合相关符号
元素与集合的关系
| 名称 | 符号 | 效果 |
|---|---|---|
| 属于 | \in | $\in$ |
| 不属于 | \notin | $\notin$ |
集合与集合相关的关系
| 名称 | 符号 | 效果 |
|---|---|---|
| 空集 | \emptyset | $\emptyset$ |
| 子集 | \subset | $\subset$ |
| 真子集 | \subseteq | $\subseteq$ |
| 交集 | \bigcap和\cap | $\bigcap$和$\cap$ |
| 并集 | \bigcup和\cup | $\bigcup$和$\cup$ |
数学重音和上下括号
数学符号可以像文字一样加重音,比如对时间求导的符号$\dot{r}$(\dot{r})、$ddot{r}$(ddot{r})、表示向量的箭头$vec{r}$(vec{r})、表示欧式空间单位向量的$\hat{\mathbf{e}}$(\hat{\mathbf{e}})等,详见表4.9。使用时要注意重音符号的作用区域,一般应当对某个符号而不是不符号加下表使用重音:
1 | $\bar{x_0} \quad \bar{x}_0$\\[5pt] |
$\bar{x_0} \quad \bar{x}_0$
$\vec{x_0} \quad \vec{x}_0$
$\hat{\mathbf{e}_x} \quad
\hat{\mathbf{e}}_x$
LATEX也能为多个字符加重音,包括直接画线的\overline和\underline命令(可叠加使用)、宽重音符号\widehat、表示向量的箭头\overrightarrow等。后两者详见表4.9和4.11等。
1 | $0.\overline{3} = |
$0.\overline{3} =
\underline{\underline{1/3}}$
$\hat{XY} \qquad \widehat{XY}$
$\vec{AB} \qquad
\overrightarrow{AB}$
\overbrace和\underbrace命令用来生成上/下括号,各自可带一个上/下标公式。
1 | $\underbrace{\overbrace{a+b+c}^6 |
$\underbrace{\overbrace{a+b+c}^6
\cdot \overbrace{d+e+f}^7}
_\text{meaning of life} = 42$
多行公式
长公式折行
通常来讲应当避免写出超过一行而需要折行的长公式。如果一定要折行的话,优先在等号之前折行,其次在加号、减号之前,再次在乘号、除号之前。其它位置应当避免折行。
amsmath宏包的multline环境提供了书写折行长公式的方便环境。它允许用\\\\(markdown中显示:\\)折行,将公式编号放在最后一行。多行公式的首行左对齐,末行右对齐,其余行居中。
因为markdown中\是转义符,所以\\才表示一个\,所以这里要写四个\(\\\\)
1 | $$ |
$$
\begin{multline}a + b + c + d + e + f+ g + h + i \\
= j + k + l + m + n\\
= o + p + q + r + s\\
= t + u + v + x + z\end{multline}
$$
与表格不同的是,公式的最后一行不写\\,如果写了,反倒会产生一个多余的空行。类似equation\*,multline\*环境排版不带编号的折行长公式。
需要注意的是,只是在Hexo的默认Markdown渲染器中才需要使用四个反斜杠
为了通用,本文下面的演示代码都使用两个反斜杠
多行公式
更多的情况是,我们需要罗列一系列公式,并令其按照等号对齐。读者可能阅读过其它手册或者资料,知道LATEX提供了eqnarray环境。它按照等号左边——等号——等号右边呈三列对齐,但等号周围的空隙过大,加上公式编号等一些bug,目前已不推荐使用
目前最常用的是align环境,它将公式用&隔为两部分并对齐。分隔符通常放在等号左边:
1 | $$ |
$$
\begin{align}
a & = b + c \\
& = d + e
\end{align}
$$
align环境会给每行公式都编号。我们仍然可以用\notag去掉某行的编号。在以下的例子,为了对齐加号,我们将分隔符放在等号右边,这时需要给等号后添加一对括号{}以产生正常的间距:
1 | $$ |
$$
\begin{align}
a ={} & b + c \\
={} & d + e + f + g + h + i+ j + k + l \notag \\
& + m + n + o \\
={} & p + q + r + s
\end{align}
$$
align还能够对齐多组公式,除等号前的&之外,公式之间也用&分隔:
1 | $$ |
$$
\begin{align}
a &=1 & b &=2 & c &=3 \\
d &=-1 & e &=-2 & f &=-5
\end{align}
$$
如果我们不需要按等号对齐,只需罗列数个公式,gather将是一个很好用的环境:
1 | $$ |
$$
\begin{gather}
a = b + c \\
d = e + f + g \\
h + i = j + k \notag \\
l + m = n
\end{gather}
$$
align和gather有对应的不带编号的版本align\*和gather\*。
公用编号的多行公式
另一个常见的需求是将多个公式组在一起公用一个编号,编号位于公式的居中位置。为此,amsmath宏包提供了诸如aligned、gathered等环境,与equation环境套用。以-ed结尾的环境用法与前一节不以-ed结尾的环境用法一一对应。我们仅以aligned举例:
1 | $$ |
$$
\begin{equation}
\begin{aligned}
a &= b + c \\
d &= e + f + g \\
h + i &= j + k \\
l + m &= n
\end{aligned}
\end{equation}
$$
split环境和aligned环境用法类似,也用于和equation环境套用,区别是split只能将每行的一个公式分两栏,aligned允许每行多个公式多栏。
公式中的间距
前文提到过,绝大部分时候,数学公式中各元素的间距是根据符号类型自动生成的,需要我们手动调整的情况极少。我们已经认识了两个生成间距的命令\quad和\qquad。在公式中我们还可能用到的间距包括\,、\:、\;以及负间距\!,其中\quad、\qquad和\,在文本和数学环境中可用,后三个命令只用于数学环境。文本中的\␣也能使用在数学公式中。
此处应该有图片,但是我的图片好像用不了了
一个常见的用途是修正积分的被积函数$f(x)$和微元$dx$之间的距离。注意微元里的$d$用的是直立体:
1 | $$ |
$$
\int_a^b f(x)\mathrm{d}x
\qquad
\int_a^b f(x),\mathrm{d}x
$$
另一个用途是生成多重积分号。如果我们直接连写两个\int,之间的间距将会过宽,此时可以使用负间距\\!修正之。不过amsmath提供了更方便的多重积分号,如**二重积分\iint、三重积分\iiint**等。
数组和矩阵
为了排版二维数组,LATEX提供了array环境,用法与tabular环境极为类似,也需要定义列格式,并用\\换行。数组可作为一个公式块,在外套用\left、\right等定界符:
1 | $$ |
还是因为是在markdown文档中\需要转义,所以两个斜杠:\\,在markdown文档中需要使用四个斜杠:\\\\来表示
$$
\mathbf{X} = \left(
\begin{array}{cccc}
x_{11} & x_{12} & \ldots & x_{1n}\\
x_{21} & x_{22} & \ldots & x_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
x_{n1} & x_{n2} & \ldots & x_{nn}\\
\end{array}
\right)
$$
值得注意的是,上一节末尾介绍的aligned等环境也可以用定界符包裹。我们还可以利用空的定界符排版出这样的效果:
1 | $$ |
$$
|x| = \left \{
\begin{array}{rl}
-x & \text{if } x < 0,\\
0 & \text{if } x = 0,\\
x & \text{if } x > 0.
\end{array} \right.
$$
我不知道这里为什么显示不正常,可以能不支持把,下面的例子同样也可额完成,衣柜对于分段函数可以写下面的这种形式。
分段函数
不过上述例子可以用amsmath提供的cases环境更轻松地完成:
1 | $$ |x| = |
$$ |x| =
\begin{cases}
-x & \text{if } x < 0,\\
0 & \text{if } x = 0,\\
x & \text{if } x > 0.
\end{cases} $$
我们当然也可以用array环境排版各种矩阵。amsmath宏包还直接提供了多种排版矩阵的环境,包括不带定界符的matrix,以及带各种定界符的矩阵pmatrix(()、bmatrix([)、Bmatrix({)、vmatrix(|)、Vmatrix(||)。使用这些环境时,无需给定列格式5:
1 | $$ |
$$
\begin{matrix}
1 & 2 \\ 3 & 4
\end{matrix} \qquad
\begin{bmatrix}
x_{11} & x_{12} & \ldots & x_{1n}\\
x_{21} & x_{22} & \ldots & x_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
x_{n1} & x_{n2} & \ldots & x_{nn}\\
\end{bmatrix}
$$
1 | $$ |
显示效果:
$$
\begin{pmatrix}
1 & 2 \\ 3 & 4
\end{pmatrix}
\qquad
\begin{bmatrix}
1 & 2 \\ 3 & 4
\end{bmatrix}
\qquad
\begin{Bmatrix}
1 & 2 \\ 3 & 4
\end{Bmatrix}
\qquad
\begin{vmatrix}
1 & 2 \\ 3 & 4
\end{vmatrix}
\qquad
\begin{Vmatrix}
1 & 2 \\ 3 & 4
\end{Vmatrix}
$$
在矩阵中的元素里排版分式时,一来要用到\dfrac等命令,二来行与行之间有可能紧贴着,这时要用到3.6.6小节的方法来调节间距:
1 | $$ |
$$
\mathbf{H}=
\begin{bmatrix}
\dfrac{\partial^2 f}{\partial x^2} &
\dfrac{\partial^2 f}
{\partial x \partial y} \\
\dfrac{\partial^2 f}
{\partial x \partial y} &
\dfrac{\partial^2 f}{\partial y^2}
\end{bmatrix}
$$
数学符号的字体控制
数学字母字体
LATEX允许一部分数学符号切换字体,主要是拉丁字母、数字等等。表4.2给出了切换字体的命令。某一些命令需要字体宏包的支持。
1 | $\mathcal{R} \quad \mathfrak{R} |
$\mathcal{R} \quad \mathfrak{R}
\quad \mathbb{R}$
$$\mathcal{L}
= -\frac{1}{4}F_{\mu\nu}F^{\mu\nu}$$
$\mathfrak{su}(2)$ and
$\mathfrak{so}(3)$ Lie algebr
数学符号的尺寸
数学符号按照符号排版的位置规定尺寸,从大到小包括行间公式尺寸、行内公式尺寸、上下标尺寸、次级上下标尺寸。除了字号有别之外,行间和行内公式尺寸下的巨算符也使用不一样的大小。LATEX为每个数学尺寸指定了一个切换的命令,见4.3。
例如行间公式的分式内,分子分母使用行内公式尺寸,巨算符采用行内尺寸的形式。对比一下分子分母使用\displaystyle命令与否的区别:
这里有一个表格
1 | $$ |
$$
P = \frac
{\sum_{i=1}^n (x_i- x)(y_i- y)}
{\displaystyle \left[
\sum_{i=1}^n (x_i-x)^2
\sum_{i=1}^n (y_i-y)^2
\right]^{1/2} }
$$
符号表
后面把这些符号表粘贴进来就行了,后面的那些不需要再看了,保留官方文档的连接,现在只要留个印象。
文本/数学模式通用符号
| 文本/数学模式通用符号 | 命令 |
|---|---|
| $\{$ | { |
| $\}$ | } |
| $\$$ | $ |
| $\%$ | % |
| $\dag$ | \dag |
| $\S$ | \S |
| $\copyright$ | \copyright |
| $\dots$ | \dots |
| $\ddag$ | \ddag |
| $\P$ | \P |
| $\pounds$ | \pounds |
二元关系符
有的二元关系符都可以加\not前缀得到相反意义的关系符,例如\not=就得到不等号(同\ne)。
| 效果 | 命令 | 效果 | 命令 | 效果 | 命令 |
|---|---|---|---|---|---|
| $<$ | < | $>$ | > | $=$ | = |
| $\leq$ | \leq or \le | $\ge$ | \geq or \ge | $\equiv$ | \equiv |
| $\ll$ | \ll | $\gg$ | \gg | $\doteq$ | \doteq |
| $\prec$ | \prec | $\succ$ | \succ | $\sim$ | \sim |
| $\preceq$ | \preceq | $\succeq$ | \succeq | $\simeq$ | \simeq |
| $\subset$ | \subset | $\supset$ | \supset | $\approx$ | \approx |
| $\subseteq$ | \subseteq | $\supseteq$ | \supseteq | $\cong$ | \cong |
| $\sqsubset$ | \sqsubset | $\sqsupset$ | \sqsupset | $\Join$ | \Join |
| $\sqsubseteq$ | \sqsubseteq | $\sqsupseteq$ | \sqsupseteq | $\bowtie$ | \bowtie |
| $\in$ | \in | $\ni$ | \ni or \owns | $\propto$ | \propto |
| $\vdash$ | \vdash | $\dashv$ | \dashv | $\models$ | \models |
| $\mid$ | \mid | $\parallel$ | \parallel | $\perp$ | \perp |
| $\smile$ | \smile | $\frown$ | \frown | $\asymp$ | \asymp |
| $:$ | : | $\notin$ | \notin | $\ne$ | \neq or \ne |
二元运算符
LaTex中的算符大多数是二元算符,除了直接用键盘可以输入的+,-,*,/外,其他符号用命令输入,常用的符号有乘号:$\times$(\times),除号: $\div$ (\div),点乘: $\cdot$ (\cdot),加减号 $\pm$ (\pm) 或者 $\mp$ (\mp)等等。更多符号命令可参考表4.7以及表4.17
图片内容
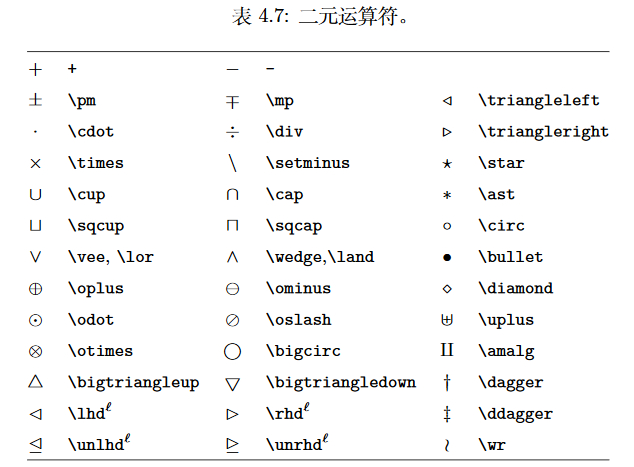
渲染效果
| latex符号 | 效果 | 描述 |
|---|---|---|
| + | $+$ | 加号 |
| - | $-$ | 减号 |
| \pm | $\pm$ | 正负号 |
| \mp | $\mp$ | 正负号 |
| \cdot | $\cdot$ | 点乘 |
| \times | $\times$ | 乘法 |
| \div | $\div$ | 除法 |
| \cup | $\cup$ | 并 |
| \cap | $\cap$ | 交集 |
| \sqcup | $\sqcup$ | 不懂叫啥 |
| \sqcap | $\sqcap$ | 不懂叫啥 |
| \vee,或者\lor | $\vee$,$\lor$ | 不懂叫啥 |
| \wedgw,或者\land | $\wedge$,$\land$ | 不懂叫啥 |
| \oplus | $\oplus$ | 异或运算 |
| \ominus | $\ominus$ | 不懂叫啥 |
| \odot | $\odot$ | 异或运算 |
| \oslash | $\oslash$ | 不懂叫啥 |
| \otimes | $\times$ | 不懂叫啥 |
| \bigtriangleup | $\bigtriangleup$ | 不懂叫啥 |
| \bigtriangledown | $\bigtriangledown$ | 不懂叫啥 |
| \triangleleft | $\triangleleft$ | 不懂叫啥 |
| \triangleright | $\triangleright$ | 不懂叫啥 |
| \star | $\star$ | 不懂叫啥 |
| \ast | $\ast$ | 不懂叫啥 |
| \circ | $\circ$ | 不懂叫啥 |
| \bigcirc | $\bigcirc$ | 不懂叫啥 |
| \bullet | $\bullet$ | 不懂叫啥 |
| \diamond | $\diamond$ | 不懂叫啥 |
| \uplus | $\uplus$ | 不懂叫啥 |
| \amalg | $\amalg$ | 不懂叫啥 |
| \dagger | $\dagger$ | 不懂叫啥 |
| \ddagger | $\ddagger$ | 不懂叫啥 |
| \wr | $\wr$ | 不懂叫啥 |
希腊字母
latex希腊字母符号代码就是斜杠+其英文名称,如$\alpha$:$\alpha$,$\beta$:$\beta$…等。
大写的latex希腊字母就是斜杠+首字母大写的英文名称,如$\Gamma$:$\Gamma$,$\Delta$:$\Delta$…。
\Alpha,\Beta等希腊字母符号不存在,因为它们和拉丁字母A,B等一模一样;小写字母里也不存在\omicron,可以直接用字母o代替,省的打那么长的代码。
希腊字母顺序表
| 序号 | 大写 | 小写 | 英文 | 读音 |
|---|---|---|---|---|
| 1 | $A$ | $\alpha$ | alpha | |
| 2 | $B$ | $\beta$ | beta | |
| 3 | $\Gamma$ | $\gamma$ | gamma | |
| 4 | $\Delta$ | $\delta$ | delta | |
| 5 | $E$ | $\epsilon$ | epsilon | |
| 6 | $Z$ | $\zeta$ | zeta | |
| 7 | $H$ | $\eta$ | eta | |
| 8 | $\Theta$ | $\theta$ | theta | |
| 9 | $I$ | $\iota$ | iota | |
| 10 | $K$ | $\kappa$ | kappa | |
| 11 | $\Lambda$ | $\lambda$ | lambda | |
| 12 | $M$ | $\mu$ | mu | |
| 13 | $N$ | $\nu$ | nu | |
| 14 | $\Xi$ | $\xi$ | xi | |
| 15 | $O$ | $\omicron$ | omicron | |
| 16 | $\Pi$ | $\pi$ | pi | |
| 17 | $P$ | $\rho$ | rho | |
| 18 | $\Sigma$ | $\sigma$ | sigma | |
| 19 | $T$ | $\tau$ | tau | |
| 20 | $\Upsilon$ | $\upsilon$ | upsilon | |
| 21 | $\Phi$ | $\phi$ | phi | |
| 22 | $X$ | $\chi$ | chi | |
| 23 | $\Psi$ | $\psi$ | psi | |
| 24 | $\Omega$ | $\omega$ | omega |
参考资料
https://baike.baidu.com/item/%E5%B8%8C%E8%85%8A%E5%AD%97%E6%AF%8D/4428067?fr=aladdin#2_1
巨算符
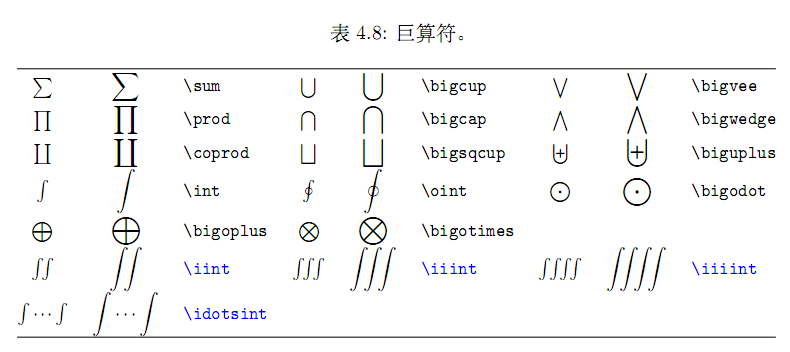
箭头
https://learnku.com/articles/46821
除了作为上下标之外,箭头还用于表示过程。amsmath的\xleftarrow和\xrightarrow命令可以为箭头增加上下标:
1 | $$ a\xleftarrow{x+y+z} b $$ |
显示效果:
$$
a\xleftarrow{x+y+z} b
$$
和
$$
c \xrightarrow [x<y]{a*b*c} d
$$
箭头详细表 图片

箭头详细表 渲染
| 效果 | 源码 | 效果 | 源码 |
|---|---|---|---|
| $\leftarrow$或者$\gets$ | \leftarrow或者\gets | $\longleftarrow$ | \longleftarrow |
| $\rightarrow$或者$\to$ | \rightarrow或者\to | $\longrightarrow$ | \longrightarrow |
| $\leftrightarrow$ | \leftrightarrow | $\longleftrightarrow$ | \longleftrightarrow |
| $\Leftarrow$ | \Leftarrow | $\Longleftarrow$ | \Longleftarrow |
| $\Rightarrow$ | \Rightarrow | $\Longrightarrow$ | \Longrightarrow |
括号和定界符
LATEX提供了多种括号和定界符表示公式块的边界。除小括号( )、中括号[ ]之外,其余都是LATEX命令,包括大括号{ }。表4.12和4.13给出了更多的括号/定界符命令。
1 | ${a,b,c} \neq \{a,b,c\}$ |
${a,b,c} \neq {a,b,c}$
使用\left和\right命令可令括号(定界符)的大小可变,在行间公式中常用。LATEX会自动根据括号内的公式大小决定定界符大小。\left和\right必须成对使用。需要使用单个定界符时,另一个定界符写成\left.或\right.。
1 | \[1 + \left(\frac{1}{1-x^{2}} |
$$
1 + \left(\frac{1}{1-x^{2}}
\right)^3 \qquad
\left.\frac{\partial f}{\partial t}
\right|_{t=0}
$$
作为重音的箭头符号

定界符

公式中的间距

参考链接
参考文献: http://texdoc.net/texmf-dist/doc/latex/lshort-chinese/lshort-zh-cn.pdf
参考链接: https://blog.csdn.net/thither_shore/article/details/52260742