11.5 实战：深入理解Graal编译器 11.5.5 代码优化与生成

发表于 更新于 分类于 ， ， ， Waline： 本文字数： 4.3k 阅读时长 ≈ 4 分钟

11.5.5 代码优化与生成

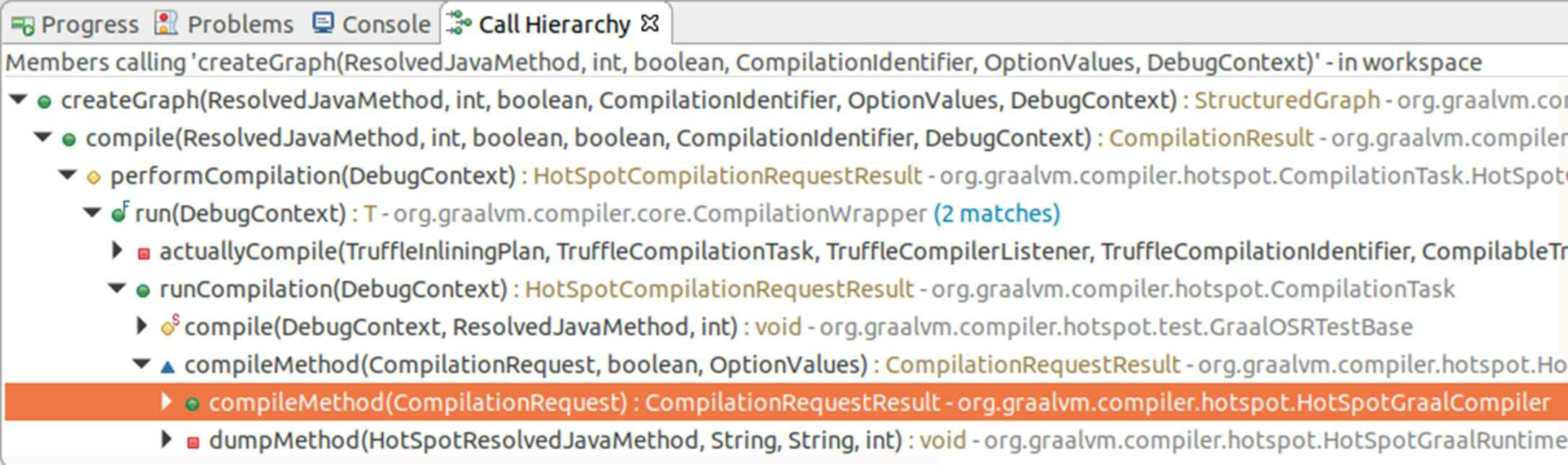
相信读者现在已经能够基本看明白Graal理想图的中间表示了，那对应到代码上，Graal编译器是如何从字节码生成理想图？又如何在理想图基础上进行代码优化的呢？这时候就充分体现出了Graal编译器在使用Java编写时对普通Java程序员来说具有的便捷性了，在Outline视图中找到创建理想图的方法是greateGraph()，我们可以从Call Hierarchy视图中轻易地找到从JVMCI的入口方法compileMethod()到greateGraph()之间的调用关系，如图11-18所示。

greateGraph()方法的代码也很清晰，里面调用了StructuredGraph::Builder()构造器来创建理想图。这 里要关注的关键点有两个：

image-20211126192125635

图11-18 构造理想图的方法

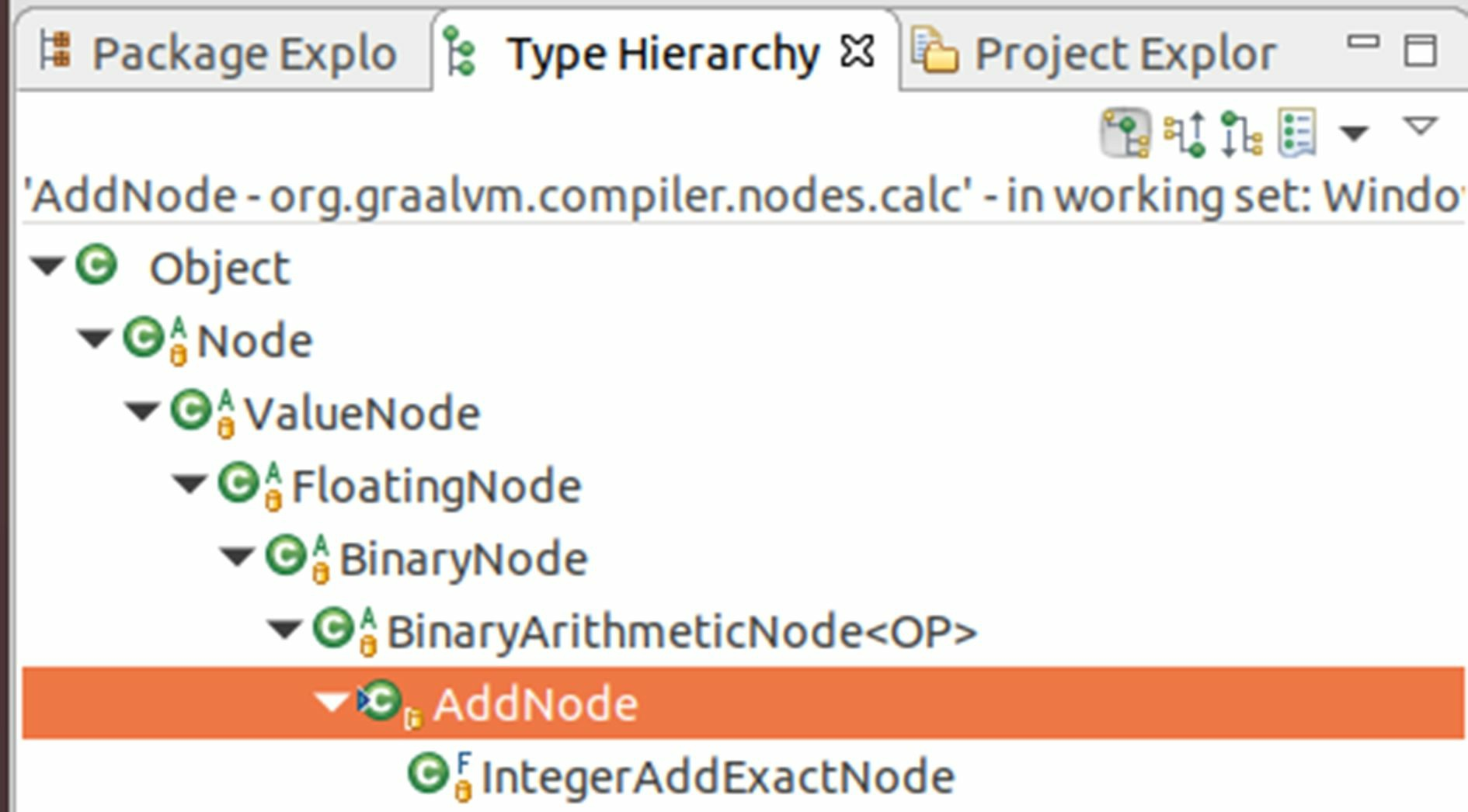
第一是理想图本身的数据结构。它是一组不为空的节点的集合，它的节点都是用ValueNode的不同类型的子类节点来表示的。仍然以x+y表达式为例，譬如其中的加法操作，就由AddNode节点来表示， 从图11-19所示的Type Hierarchy视图中可以清楚地看到加法操作是二元算术操作节点 （BinaryArithmeticNode<OP>）的一种，而二元算术操作节点又是二元操作符（BinaryNode）的一种，以此类推直到所有操作符的共同父类ValueNode（表示可以返回数据的节点）。

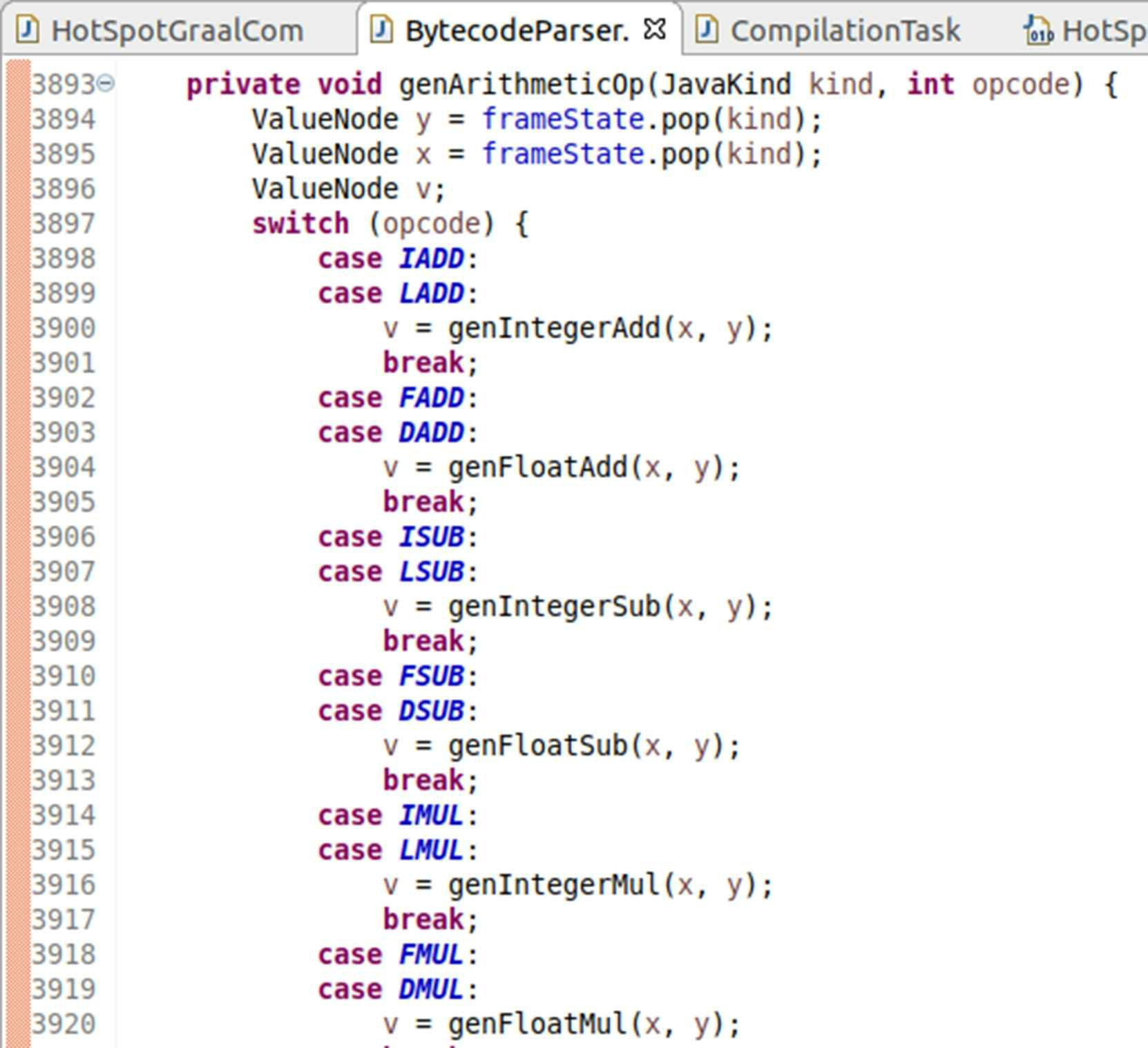
第二就是如何从字节码转换到理想图。该过程被封装在BytecodeParser类中，这个解析器我们可以按照字节码解释器的思路去理解它。如果这真的是一个字节码解释器，执行一个整数加法操作，按照 《Java虚拟机规范》所定义的iadd操作码的规则，应该从栈帧中出栈两个操作数，然后相加，再将结果入栈。而从BytecodeParser::genArithmeticOp()方法上我们可以看到，其实现与规则描述没有什么差异， 如图11-20所示。

image-20211126192231390

图11-19 节点继承关系

image-20211126192300732

图11-20 字节码解析器实现的iadd操作码

其中，genIntegerAdd()方法中就只有一行代码，即调用AddNode节点的create()方法，将两个操作数作为参数传入，创建出AddNode节点，如下所示：

1
2
3
protected ValueNode genIntegerAdd(ValueNode x, ValueNode y) {
    return AddNode.create(x, y, NodeView.DEFAULT);
}

每一个理想图的节点都有两个共同的主要操作，一个是规范化（Canonicalisation），另一个是生成机器码（Generation）。生成机器码顾名思义，就不必解释了，规范化则是指如何缩减理想图的规模，也即在理想图的基础上优化代码所要采取的措施。这两个操作对应了编译器两项最根本的任务：代码优化与代码翻译。

AddNode节点的规范化是实现在canonical()方法中的，机器码生成则是实现在generate()方法中的， 从AddNode的创建方法上可以看到，在节点创建时会调用canonical()方法尝试进行规范化缩减图的规模，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static ValueNode create(ValueNode x, ValueNode y, NodeView view) {
    BinaryOp<Add> op = ArithmeticOpTable.forStamp(x.stamp(view)).getAdd();
    Stamp stamp = op.foldStamp(x.stamp(view), y.stamp(view));
    ConstantNode tryConstantFold = tryConstantFold(op, x, y, stamp, view);
    if (tryConstantFold != null) {
        return tryConstantFold;
    }
    if (x.isConstant() && !y.isConstant()) {
        return canonical(null, op, y, x, view);
    }
    else {
        return canonical(null, op, x, y, view);
    }
}

从AddNode的canonical()方法中我们可以看到为了缩减理想图的规模而做的相当多的努力，即使只是两个整数相加那么简单的操作，也尝试过了常量折叠（如果两个操作数都为常量，则直接返回一个常量节点）、算术聚合（聚合树的常量子节点，譬如将(a+1)+2聚合为a+3）、符号合并（聚合树的相反符号子节点，譬如将(a-b)+b或者b+(a-b)直接合并为a）等多种优化，canonical()方法的内容较多，请读者自行参考源码，为节省版面这里就不贴出了。

对理想图的规范化并不局限于单个操作码的局部范围之内，很多的优化都是要立足于全局来进行的，这类操作在CanonicalizerPhase类中完成。仍然以上一节的公共子表达式消除为例，这就是一个全局性的优化，实现在CanonicalizerPhase::tryGlobalValueNumbering()方法中，其逻辑看起来已经非常清晰了：如果理想图中发现了可以进行消除的算术子表达式，那就找出重复的节点，然后替换、删除。具体代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
public boolean tryGlobalValueNumbering(Node node, NodeClass<?> nodeClass) {
    if (nodeClass.valueNumberable()) {
        Node newNode = node.graph().findDuplicate(node);
        if (newNode != null) {
            assert !(node instanceof FixedNode || newNode instanceof FixedNode);
            node.replaceAtUsagesAndDelete(newNode);
            COUNTER_GLOBAL_VALUE_NUMBERING_HITS.increment(debug);
            debug.log("GVN applied and new node is %1s", newNode);
            return true;
        }
    }
    return false;
}

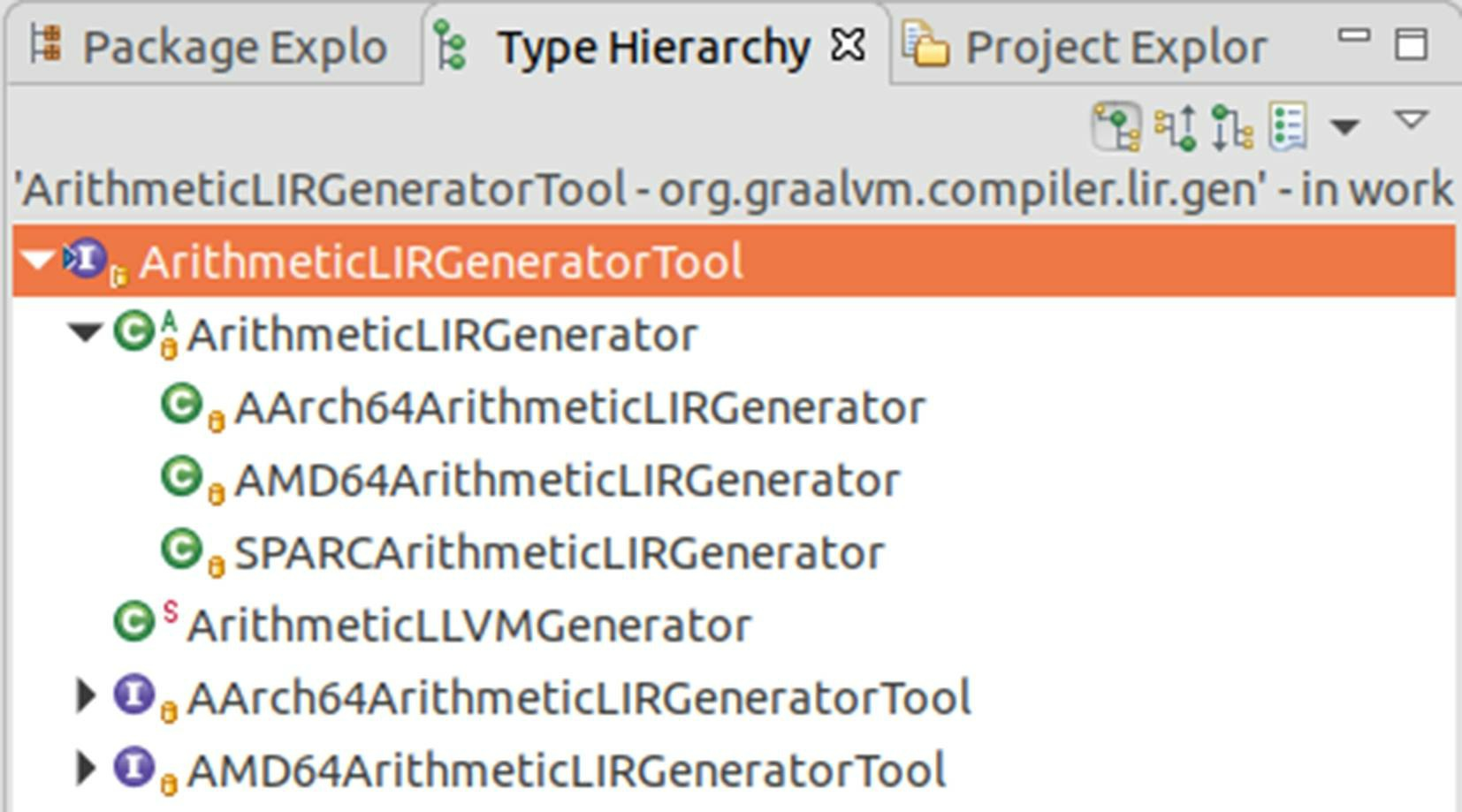
至于代码生成，Graal并不是直接由理想图转换到机器码，而是和其他编译器一样，会先生成低级中间表示（LIR，与具体机器指令集相关的中间表示），然后再由HotSpot统一后端来产生机器码。譬如涉及算术运算加法的操作，就在ArithmeticLIRGeneratorTool接口的emitAdd()方法里完成。从低级中间表示的实现类上，我们可以看到Graal编译器能够支持的目标平台，目前它只提供了三种目标平台的指令集（SPARC、x86-AMD64、ARMv8-AArch64）的低级中间表示，所以现在Graal编译器也就只能支持这几种目标平台，如图11-21所示。

image-20211126192556614

图11-21 Graal支持的目标平台生成器

为了验证代码阅读的成果，现在我们来对AddNode的代码生成做一些小改动，将原本生成加法汇编指令修改为生成减法汇编指令，即按如下方式修改AddNode::generate()方法：

1
2
3
4
5
class AddNode {
    void generate(...) {
        ... gen.emitSub(op1, op2, false) ...// 原来这个方法是emitAdd()
    }
}

然后在虚拟机运行参数中加上-XX：+PrintAssembly参数，因为从低级中间表示到真正机器码的转换是由HotSpot统一负责的，所以11.2节中用到的HSDIS插件仍然能发挥作用，帮助我们输出汇编代码。从输出的汇编中可以看到，在没有修改之前，AddNode节点输出的汇编代码如下所示：

1
2
3
4
5
6
7
8
9
0x000000010f71cda0:     nopl    0x0(%rax,%rax,1) 
0x000000010f71cda5:     add     %edx,%esi       ;*iadd {reexecute=0 rethrow=0 return_oop=0} 
                                                ; - Demo::workload@2 (line 10) 
0x000000010f71cda7:     mov     %esi,%eax       ;*ireturn {reexecute=0 rethrow=0 return_oop=0} 
                                                ; - Demo::workload@3 (line 10) 
0x000000010f71cda9:     test    %eax,-0xcba8da9(%rip) # 0x0000000102b74006 
                                                ; {poll_return} 
0x000000010f71cdaf:     vzeroupper 
0x000000010f71cdb2:     retq

而被我们修改后，编译的结果已经变为：

1
2
3
4
5
6
7
8
9
0x0000000107f451a0:  nopl    0x0(%rax,%rax,1) 
0x0000000107f451a5:  sub     %edx,%esi  ;*iadd {reexecute=0 rethrow=0 return_oop=0}
                                        ; - Demo::workload@2 (line 10) 
0x0000000107f451a7:  mov     %esi,%eax  ;*ireturn {reexecute=0 rethrow=0 return_oop=0}
                                        ; - Demo::workload@3 (line 10) 
0x0000000107f451a9:  test    %eax,-0x1db81a9(%rip)      # 0x000000010618d006 
                                        ; {poll_return} 
0x0000000107f451af:  vzeroupper 
0x0000000107f451b2:  retq

我们的修改确实促使Graal编译器产生了不同的汇编代码，这也印证了我们代码分析的思路是正确的。写到这里，笔者忍不住感慨，Graal编译器的出现对学习和研究虚拟机代码编译技术实在有着不可估量的价值。在本书第2版编写时，只有C++编写的复杂无比的服务端编译器，要进行类似的实战是非常困难的，即使勉强写出来，也会因为过度烦琐而失去阅读价值。