11.5 实战：深入理解Graal编译器 11.5.4 代码中间表示

11.5.4 代码中间表示

Graal编译器在设计之初就刻意采用了与HotSpot服务端编译器一致（略有差异但已经非常接近） 的中间表示形式，也即是被称为Sea-of-Nodes的中间表示，或者与其等价的被称为理想图（Ideal Graph，在代码中称为Structured Graph）的程序依赖图（Program Dependence Graph，PDG）形式。在11.2节即时编译器的实战中，我们已经通过可视化工具Ideal Graph Visualizer看到过在理想图上翻译和优化输入代码的整体过程，从编译器内部来看即：字节码→理想图→优化→机器码（以Mach Node Graph表示）的转变过程。在那个实战里面，我们着重分析的是理想图转换优化的整体过程，对于多数读者，尤其是不熟悉编译原理与编译器设计的读者，可能会不太容易读懂每个阶段所要做的工作。 在本节里面，我们以例子和对照Graal源码的形式，详细讲解输入代码与理想图的转化对应关系，以便读者理解Graal是如何基于理想图去优化代码的。

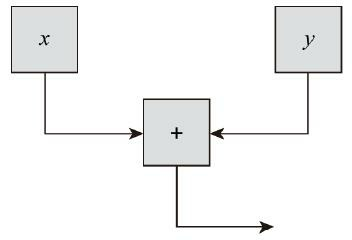
理想图是一种有向图，用节点来表示程序中的元素，譬如变量、操作符、方法、字段等，而用边来表示数据或者控制流。我们先从最简单的例子出发。譬如有一个表达式：x+y，在理想图中可以表示为x、y两个节点的数据流流入加法操作符，表示相加操作读取了x、y的值，流出的便则表示数据流的流向，即相加的结果会在哪里被使用，如图11-13所示。

图11-13 构造理想图（1）

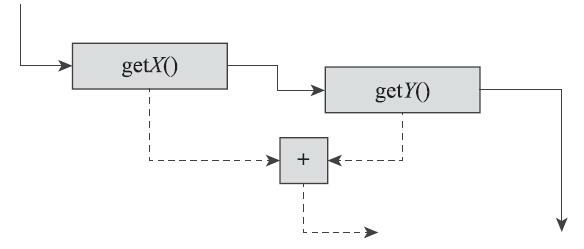
这很容易接受吧？那我们把例子稍微复杂化一些，把表达式x+y变为getX()+getY()，仍是用理想图表达其计算过程，这时候除了数据流向之外，还必须要考虑方法调用的顺序。在理想图中用另外一条边来表示方法的调用（为了便于区分，数据流笔者使用蓝色线（以虚线表示），控制流使用红色线 （以实线表示）），说明代码的执行顺序是先调用getX()方法，再调用getY()方法，如图11-14所示。

图11-14 构造理想图（2）

以上这些简单的前置知识就已经足以支撑我们本次实战的进行了，理想图本质上就是这种将数据流图和控制流图以某种方式合并到一起，用一种边来表示数据流向，另一种边来表示控制流向的图形表示。

现在我们在代码清单11-15或者代码清单11-16所示的基础上再增加一个参数-Dgraal.Dump，要求Graal编译器把构造的理想图输出出来，加入后编译时将会产生类似如下的输出，提示了生成的理想图的存储位置：

[Use -Dgraal.LogFile=<path> to redirect Graal log output to a file.] 
Dumping IGV graphs in /home/icyfenix/develop/eclipse-workspace/A_GraalTest/graal_dumps/2019.08.18.16.51.23.073

我们可以使用mx igv命令来获得能够支持Graal编译器生成的理想图格式的新版本的Ideal Graph Visualizer工具^1，我们以下面这段简单代码的理想图的表示为例子：

int average(int a, int b) {
    return (a + b) / 2;
}

在Ideal Graph Visualizer工具中，将显示图11-15所示的样式的理想图。

图11-15 构造理想图（3）

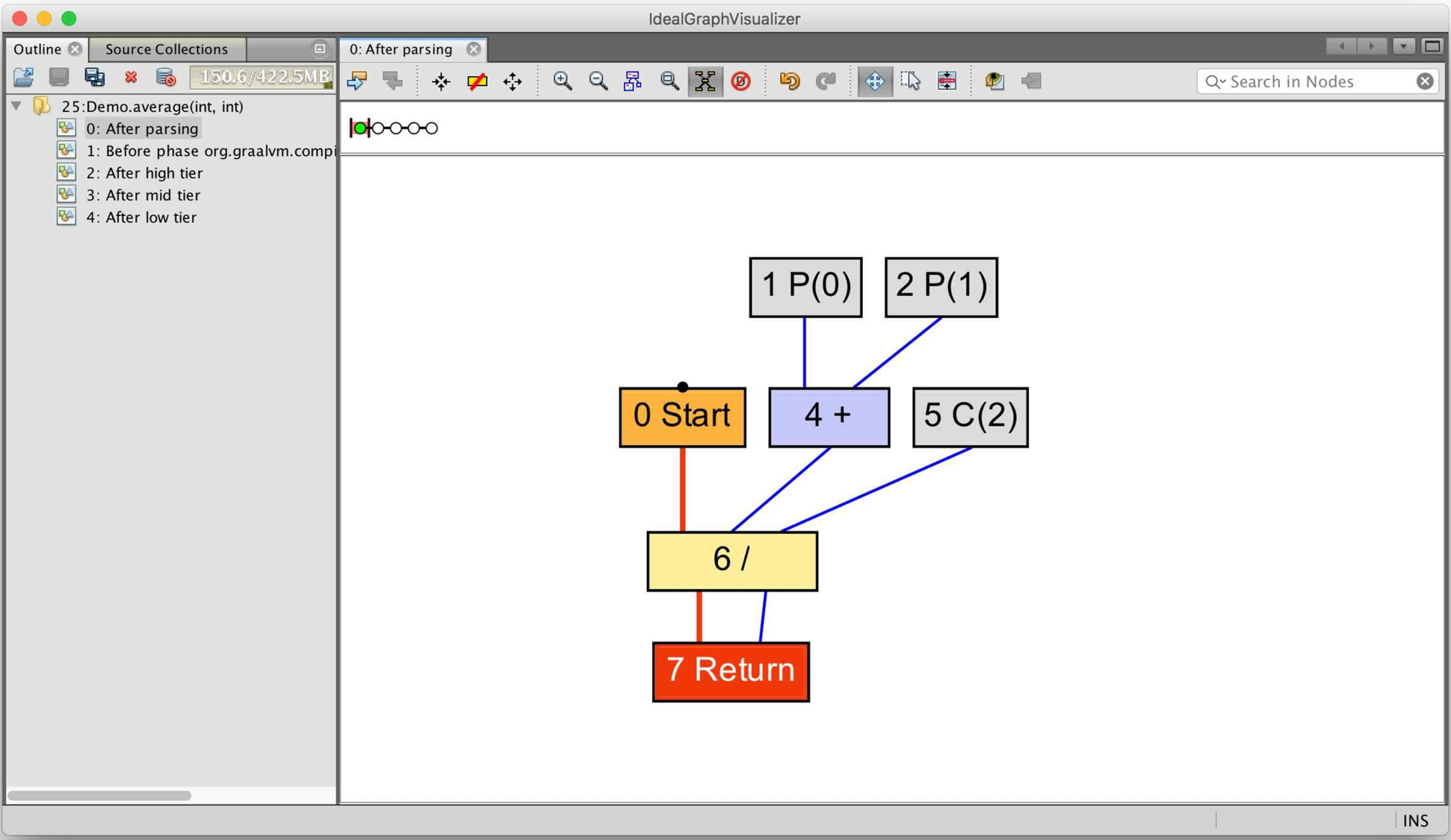
与图11-11和图11-12所示相比，虽然没有了箭头，但是节点上列明了代表执行顺序的序号，仍然是蓝色线表示数据流、红色线表示控制流。从图中可以看到参数0（记作P(0)）和参数1（记作P(1)）是如何送入加法操作的，然后结果是如何和常量2（记作C(2)）一起送入除法操作的。

再下一步我们就会开始接触真实的代码编译和优化了。前面介绍编译器优化技术时提到过公共子表达式消除，那我们来设计代码清单11-17所示的两段代码。

代码清单11-17 公共子表达式被消除的应用范围

// 以下代码的公共子表达式能够被消除
int workload(int a, int b) {
    return (a + b) * (a + b);
}
// 以下代码的公共子表达式是不可以被消除的
int workload() {
    return (getA() + getB()) * (getA() + getB());
}

对于第一段代码，a+b是公共子表达式，可以通过优化使其只计算一次而不会有任何的副作用。但是对于第二段代码，由于getA()和getB()方法内部所蕴含的操作是不确定的，它是否被调用、调用次数的不同都可能会产生不同返回值或者其他影响程序状态的副作用（譬如改变某个全局的状态变量）， 这种代码只能内联了getA()和getB()方法之后才能考虑更进一步的优化措施，仍然保持函数调用的情况下是无法做公共子表达式消除的。我们可以从Graal生成的理想图中清晰地看到这一点，对于第一段代码，生成的理想图如图11-16所示。

图11-16 构造理想图（4）

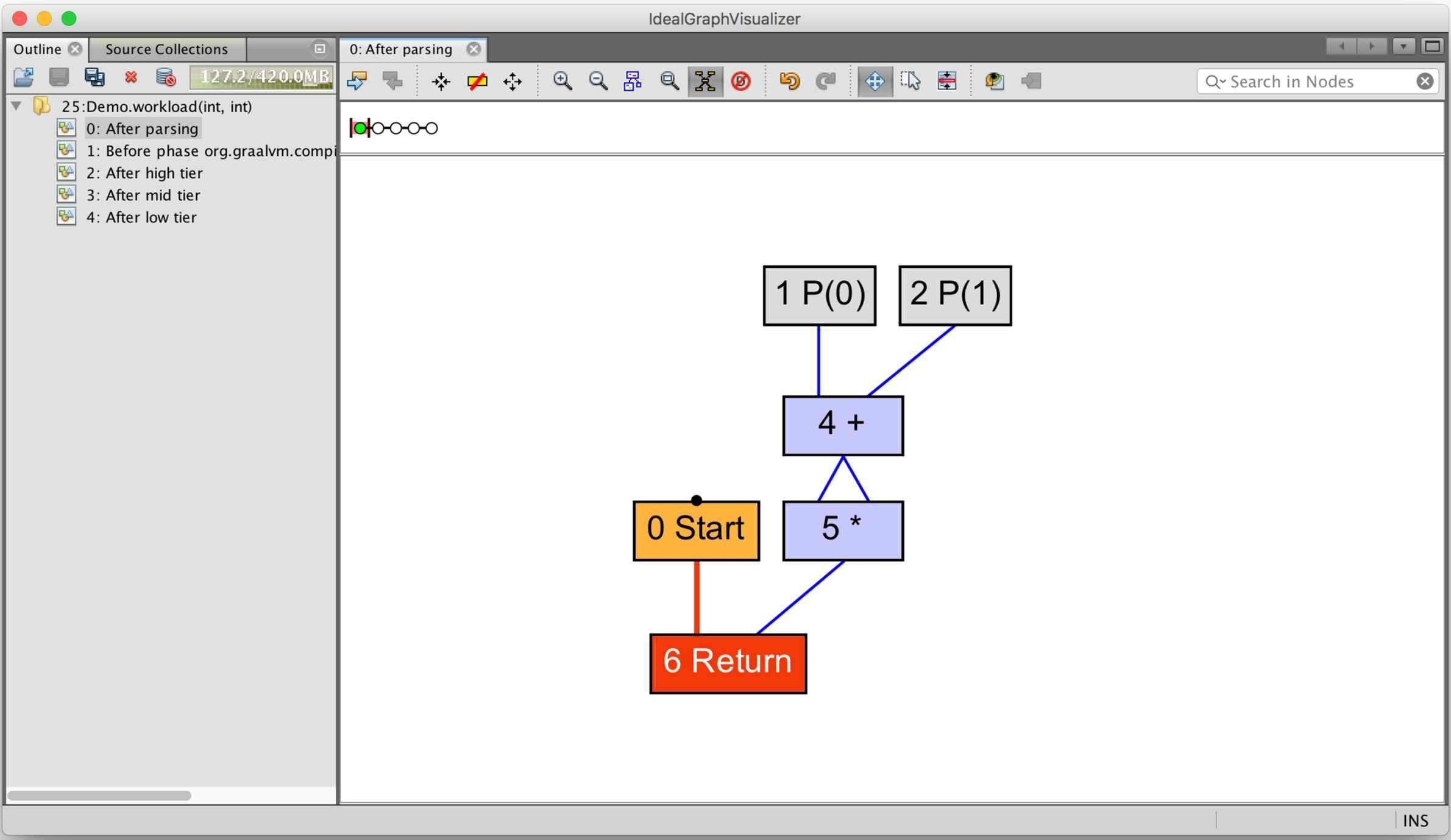
从图11-16所示中可以看到，参数1、2的加法操作只进行了一次，然后同时流出了两条数据流指向乘法操作的输入中。而如果是第二段代码，则生成的理想图如图11-17所示。

图11-17 构造理想图（5）

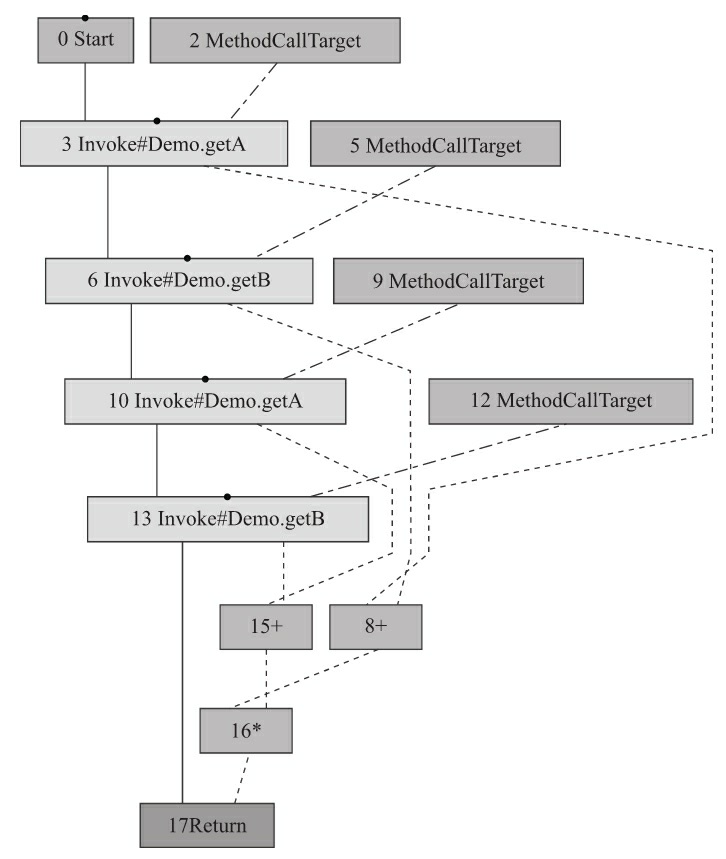
从图中代表控制流的红色边（以实线表示）可以看出，四次方法调用全部执行了，代表数据流的蓝色边（以虚线表示）也明确看到了两个独立加法操作节点，由此看出这个版本是不会把它当作公共子表达式来消除的。